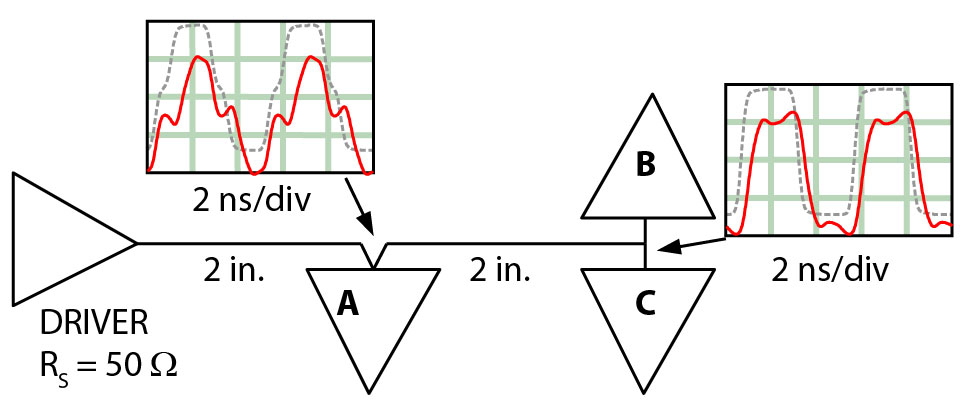
What's That Glitch?
Have you ever seen a glitch such as the one at Gate A in Figure 1? This non-monotonic glitch appears symmetrically in both rising and falling edges, although that scenario is not always the case. Can you guess what causes it?
If you have a simulator handy, here's some data for your calculations. The clock-distribution network in Figure 1 operates at 200 MHz. The 50-Ω driver generates symmetrical 400-psec rise and fall times.
The trace from the driver to Point A is a controlled-impedance trace routed between solid reference planes. It has a characteristic impedance of Z0=50 Ω and an effective dielectric constant of 4.3. The trace is 2 in. long, making a raw, unloaded trace delay of 351 psec. The same parameters apply to the other trace segment leading from the first load at A to the double loads at B and C. Loads B and C lie so close together (compared with the signal rise time) that it isn't worth worrying about the length separating them.
Given this information and assuming a perfect driver package (that is, no significant inductance), the circuit should act as a perfectly normal series-terminated line. The expected waveforms appear as gray lines in Figure 1. The waveform at A exhibits some slight hesitancy at the center line (corresponding to the 702-psec round trip to the end of the line and back) but nothing of major concern.
Now add to your receiver the crucial piece of information: a receiver-input capacitance of 3 pF (per receiver). When you add the receiver capacitance to your simulator, it produces the glitch-laden waveforms in Figure 1 (solid red lines). If you guessed that load capacitance causes the difficulties in this example, you guessed correctly.
Can you safely conclude that capacitive loading always produces glitches? Not always, but these three principles hold true:
- Capacitive loads produce lumpy waveforms.
- The bigger the capacitance, the bigger the lumps.
- Big lumps in the wrong place cause big problems.
You can organize these principles into guidelines for routing. First, when placing a capacitive load, CL, on an otherwise perfectly good transmission structure, always take a moment to mentally compute the capacitive time constant, (1/2)Z0CL. Whenever this constant approaches a significant fraction of your signal rise time, expect to see big lumps in the resulting waveform. Taking Figure 1 as an example, one-half the line impedance of 50 Ω times the total double-load capacitance of 6 pF produces a time constant of 150 psec. This time constant represents roughly one-third of the signal rise time. When considering signal quality, that's a big effect.
Second, consider the location of your capacitive loads. If more than one-half the rise time separates the loads, you increase the probability that the lumps that one load generates will end up in the wrong place, at the wrong time, at the other load position. In the current example, without changing the total transmission-path length, try sliding A to the left, closer to the source and further away from load combination B/C. That change worsens the glitch. Conversely, sliding A toward the endpoint improves things. In general, scrunching all the loads toward the end of a series-terminated structure almost always works the best.
Figure 1—Reflections from the double-load capacitance at B/C cause glitches at A.